Eigenvalue Problems

An eigenvalue problem is a matrix equation of the form

: $\mathbf{A} \vec{x} = \lambda \vec{x},$

where $\mathbf{A}$ is a known $N\times N$ matrix. The problem is to find one (or more than one) non-zero vector $\vec{x}$ , which is called an eigenvector, and the associated $\lambda \in \mathbb{C}$ , which is called an eigenvalue. Eigenvalue problems are ubiquitous in practically all fields of physics. Most prominently, they are used to describe the "modes" of a physical system, such as the modes of a classical mechanical oscillator, or the energy states of an atom.

Before discussing numerical solutions to the eigenvalue problem, let us quickly review the relevant mathematical facts.

Basic facts about eigenvalue problems

Even if a matrix $\mathbf{A}$ is real, its eigenvectors and eigenvalues can be complex. For example,

: $\begin{bmatrix}1&1\\-1&1\end{bmatrix} \begin{bmatrix}1\\i\end{bmatrix} = (1+i) \begin{bmatrix}1\\i\end{bmatrix}.$

Eigenvectors are not uniquely defined. Given an eigenvector $\vec{x}$ , any nonzero complex multiple of that vector is also an eigenvector of the same matrix, with the same eigenvalue. We can reduce this ambiguity by normalizing eigenvectors to a fixed unit length:

: $\sum_{n=0}^{N-1} |x_n|^2 = 1.$

Note, however, that even after normalization, there is still an inherent ambiguity in the overall complex phase. Multiplying a normalized eigenvector by any phase factor $e^{i\phi}$ gives another normalized eigenvector with the same eigenvalue.

Matrix diagonalization

Most matrices are diagonalizable, meaning that their eigenvectors span the 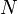$N$ -dimensional complex space (where 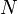$N$ is the matrix size). Matrices which are not diagonalizable are called defective. Many classes of matrices that are relevant to physics (such as Hermitian matrices) are always diagonalizable; i.e., never defective.

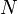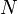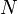The reason for the term "diagonalizable" is as follows. A diagonalizable $N\times N$ matrix $\mathbf{A}$ has eigenvectors that span the $N$ -dimensional space, meaning that we can choose $N$ linearly independent eigenvectors, $\{\vec{x}_0, \vec{x}_1, \cdots \vec{x}_{N-1}\}$ , with eigenvalues $\{\lambda_0, \lambda_1, \cdots \lambda_{N-1}\}$ . We refer to such a set of $N$ eigenvalues as the "eigenvalues of $\mathbf{A}$ ". If we group the eigenvectors into an $N\times N$ matrix

: $\mathbf{Q} = [\vec{x}_0, \vec{x}_1, \cdots \vec{x}_{N-1}],$

then, since the eigenvectors are linearly independent, $\mathbf{Q}$ is guaranteed to be invertible. Using the eigenvalue equation, we can then show that

: $\mathbf{Q}^{-1} \,\mathbf{A} \, \mathbf{Q} = \begin{bmatrix}\lambda_0 & 0& \cdots & 0 \\ 0 & \lambda_1 & \cdots & 0 \\ \vdots& \vdots & \ddots & \vdots \\ 0&0&\cdots&\lambda_{N-1}\end{bmatrix}.$

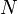In other words, there exists a similarity transformation which converts $\mathbf{A}$ into a diagonal matrix. The $N$ numbers along the diagonal are precisely the eigenvalues of $\mathbf{A}$ .

The characteristic polynomial

One of the most important consequences of diagonalizability is that the determinant of a diagonalizable matrix $\mathbf{A}$ is the product of its eigenvalues:

: $\det(\mathrm{A}) = \prod_{n=0}^{N-1} \lambda_n$

This can be proven by taking the determinant of the similarity transformation equation, and using (i) the property of the determinant that $\det(\mathbf{U}\mathbf{V}) = \det(\mathbf{U})\det(\mathbf{V})$ , and (ii) the fact that the determinant of a diagonal matrix is the product of the elements along the diagonal.

In particular, the determinant of $\mathbf{A}$ is zero if one of its eigenvalues is zero. This fact can be further applied to the following re-arrangement of the eigenvalue equation:

: $\Big(\mathbf{A} - \lambda\mathbf{I}\Big) \, \vec{x} = 0,$

where $\mathbf{I}$ is the $N\times N$ identity matrix. This says that the matrix $\mathbf{A}-\lambda\mathbf{I}$ has an eigenvalue of zero, meaning that for any eigenvalue $\lambda$ ,

: $\det\left(\mathbf{A} - \lambda\mathbf{I}\right) = 0.$

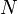The left-hand side of the above equation is a polynomial in the variable $\lambda$ , of degree $N$ . This is called the characteristic polynomial of the matrix $\mathbf{A}$ . Its roots are eigenvalues of $\mathbf{A}$ , and vice versa.

For $2\times2$ matrices, the standard way of calculating the eigenvalues is to find the roots of the characteristic polynomial. However, this is not a reliable method for finding the eigenvalues of larger matrices. There is a well-known and important result in mathematics, known as Abel's impossibility theorem, which states that polynomials of degree 5 and higher have no general algebraic solution. (By comparison, degree-2 polynomials have a general algebraic solution, which is the familiar quadratic formula, and similar formulas exist for degree-3 and degree-4 polynomials.) A matrix of size $N \ge 5$ has a characteristic polynomial of degree $N \ge 5$ , and Abel's impossibility theorem tells us that we can't calculate the roots of that characteristic polynomial by ordinary arithmetic.

In fact, Abel's impossibility theorem leads to an even stronger conclusion: there is no general algebraic method for finding the eigenvalues of a matrix of size $N \ge 5$ , whether using the characteristic polynomial or any other method. For suppose we had such a method for finding the eigenvalues of a matrix. Then, for any polynomial equation of degree $N \ge 5$ , of the form

: $a_0 + a_1 \lambda + \cdots + a_{N-1} \lambda^{N-1} + \lambda^N = 0,$

we can construct an $N\times N$ "companion matrix" of the form

: $\mathbf{A} = \begin{bmatrix}0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1& \cdots & 0 \\ \vdots&\vdots&\ddots&\ddots& \vdots \\ 0&0&0&\ddots&1\\-a_0& -a_1& -a_2 & \cdots & -a_{N-1} \end{bmatrix}.$

As you can check for yourself, each root $\lambda$ of the polynomial is also an eigenvalue of the companion matrix, with corresponding eigenvector

: $\vec{x} = \begin{bmatrix}1\\\lambda\\ \vdots \\ \lambda^{N-1}\end{bmatrix}.$

Hence, if there exists a general algebraic method for finding the eigenvalues of a large matrix, that would allow us to find solve polynomial equations of high degree. Abel's impossibility theorem tells us that no such solution method can exist.

This might seem like a terrible problem, but in fact there's a way around it, as we'll shortly see.

Hermitian matrices

A Hermitian matrix $\mathbf{H}$ is a matrix which has the property

: $\mathbf{H}^\dagger = \mathbf{H},$

where $\mathbf{H}^\dagger$ denotes the "Hermitian conjugate", which is matrix transposition accompanied by complex conjugation:

: $\mathbf{H}^\dagger \equiv \left(\mathbf{H}^T\right)^*, \quad \mathrm{i.e.}\;\; \left(H^\dagger\right)_{ij} = H_{ji}^*.$

Hermitian matrices have the nice property that all their eigenvalues are real. This can be easily proven using index notation:

: $\begin{align}\sum_j H_{ij} x_j = \lambda x_i \;\;&\Rightarrow\;\; \sum_j x_j^* H_{ji} = \lambda^* x_i^*\\ &\Rightarrow \sum_{ij} x^*_i H_{ij} x_j = \lambda \sum_i |x_i|^2 = \lambda^* \sum_j |x_j|^2 \\ &\Rightarrow \lambda = \lambda^*.\end{align}$

In quantum mechanics, Hermitian matrices play a special role: they represent measurement operators, and their eigenvalues (which are restricted to the real numbers) are the set of possible measurement outcomes.

Numerical eigensolvers

As discussed above, Abel's impossibility theory tells us that there is no general algebraic formula for calculating the eigenvalues of an $N\times N$ matrix, for $N\ge 5$ . In practice, however, there exist numerical methods, called eigensolvers, which can compute eigenvalues (and eigenvectors) even for very large matrices, with hundreds of rows/columns, or larger. How could this be?

The answer is that numerical eigensolvers are approximate, not exact. But even though their results are not exact, they are very precise—they can approach the exact eigenvalues to within the fundamental precision limits of floating-point arithmetic. Since we're limited by those floating-point precision limits anyway, that's good enough!

Sketch of the eigensolver method

We will not go into detail about how numerical eigensolvers work, as that would involve a rather long digression. For those interested, the following paper provides a good pedagogical presentation of the subject:

Bruno Lang, Direct Solvers for Symmetric Eigenvalue Problems. Modern Methods and Algorithms of Quantum Chemistry, Proceedings, Second Ed. (2000). PDF download link

Here is a very brief sketch of the basic method. Similar to Gaussian elimination, the algorithm contains two phases, a relatively costly/slow initial phase and a relatively fast second phase. The first phase, which is called Householder reduction, applies a carefully-chosen set of similarity transformations to the input matrix $\mathbf{A}_0$ :

: $\mathbf{A}_0 \;\rightarrow \;\mathbf{A}_1 = \mathbf{X}_1^{-1} \mathbf{A}_0 \mathbf{X}_1 \;\rightarrow \; \mathbf{A}_2 = \mathbf{X}_2^{-1} \mathbf{A}_1 \mathbf{X}_2, \;\; \mathrm{etc.}$

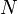The end result is a matrix $\mathbf{A}_k$ which is in Hessenberg form: the elements below the first subdiagonal are all zero (the elements immediately below the main diagonal, i.e. along the first subdiagonal, are allowed to be nonzero). The entire Householder reduction phase requires $O(N^3)$ arithmetic operations, where $N$ is the size of the matrix.

The second phase of the algorithm is called QR iteration. Using a different type of similarity transformation, the elements along the subdiagonal of the Hessenberg matrix are reduced in magnitude. When these elements become negligible, the matrix becomes upper-triangular; in that case, the eigenvalues are simply the elements along the diagonal.

The QR process is iterative, in that it progressively reduces the magnitude of the matrix elements along the subdiagonal. Formally, an infinite number of iterations would be required to reduce these elements to zero—that's why Abel's impossibility theorem isn't violated! In practice, however, QR iteration converges extremely quickly, so this phase ends up taking only $O(N^2)$ time.

Hence, the overall runtime for finding the eigenvalues of a matrix scales as $O(N^3)$ . The eigenvectors can also be computed as a side-effect of the algorithm, with no extra increase in the runtime scaling.

Python implementation

There are four main numerical eigensolvers implemented in Scipy, which are all found in the scipy.linalg package:

scipy.linalg.eig returns the eigenvalues and eigenvectors of a matrix.
scipy.linalg.eigvals returns the eigenvalues (only) of a matrix.
scipy.linalg.eigh returns the eigenvalues and eigenvectors of a Hermitian matrix.
scipy.linalg.eigvalsh returns the eigenvalues (only) of a Hermitian matrix.

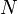The reason for having four separate functions is efficiency. The runtimes of all four functions scale as $O(N^3)$ , but for each $N$ the actual runtimes of eigvals and eigvalsh will be shorter than eig and eigh, because the eigensolver is only asked to find the eigenvalues and need not construct the eigenvectors. Furthermore, eigvalsh is faster than eigvals, and eigh is faster than eig, because the eigensolver algorithm can make use of certain numerical shortcuts which are valid only for Hermitian matrices.

If you pass eigvalsh or eigh a matrix that is not actually Hermitian, the results are unpredictable; the function may return a wrong value without signaling any error. Therefore, you should only use these functions if you are sure that the input matrix is definitely Hermitian (which is usually because you constructed the matrix that way); if the mtrix is Hermitian, eigvalsh or eigh are certainly preferable to use, because they run faster than their non-Hermitian counterparts.

Here is a short program that uses eigvals to find the eigenvalues of a $3\times3$ matrix:

from scipy import *
import scipy.linalg as lin

A = array([[1,3,1],[1, 3, 4],[2, 4, 2]])
lambd = lin.eigvals(A)

print(lambd)

Running the program outputs:

[ 7.45031849+0.j         -0.72515925+0.52865751j -0.72515925-0.52865751j]

The return value of eigvals is a 1D array of complex numbers, storing the eigenvalues of the input. The eigvalsh function behaves similarly, except that a real array is returned (since Hermitian matrices have real eigenvalues). Note: we cannot use lambda as the name of a variable, because lambda is reserved as a special keyword in Python.

Here is an example of using eig:

>>> A = array([[1,3,1],[1, 3, 4],[2, 4, 2]])
>>> lambd, Q = lin.eig(A)
>>> lambd
array([ 7.45031849+0.j    , -0.72515925+0.52865751j,   -0.72515925-0.52865751j])
>>> Q
array([[ 0.40501343+0.j        ,  0.73795979+0.j        ,  0.73795979-0.j        ],
       [ 0.65985810+0.j        , -0.51208724+0.22130102j, -0.51208724-0.22130102j],
       [ 0.63289132+0.j        ,  0.26316357-0.27377508j,  0.26316357+0.27377508j]])

The eig function returns a pair of values; the first is a 1D array of eigenvalues (which we name lambd in the above example), and the second is a 2D array containing the corresponding eigenvectors in each column (which we name Q). For example, the first eigenvector can be accessed with Q[:,0]. We can verify that this is indeed an eigenvector:

>>> dot(A, Q[:,0])
array([ 3.01747903+0.j,  4.91615298+0.j,  4.71524187+0.j])
>>> lambd[0] * Q[:,0]
array([ 3.01747903+0.j,  4.91615298+0.j,  4.71524187+0.j])

The eigh function behaves similarly, except that the 1D array of eigenvalues is real.

Generalized eigenvalue problem

Sometimes, you might also come across generalized eigenvalue problems, which have the form

: $\mathbf{A}\, \vec{x} = \lambda\, \mathbf{B}\, \vec{x},$

for known equal-sized square matrices $\mathbf{A}$ and $\mathbf{B}$ . We call $\lambda$ a "generalized eigenvalue", and $\vec{x}$ a "generalized eigenvector", for the pair of matrices $(\mathbf{A},\mathbf{B})$ . The generalized eigenvalue problem reduces to the ordinary eigenvalue problem when $\mathbf{B}$ is the identity matrix.

The naive way to solve the generalized eigenvalue problem would be to compute the inverse of $\mathbf{B}^{-1}$ , and then solve the eigenvalue problem for $\mathbf{B}^{-1}\mathbf{A}$ . However, it turns out that the generalized eigenvalue problem can be solved directly with only slight modifications to the usual numerical eigensolver algorithm. In fact, the Scipy eigensolvers described in the previous section will solve the generalized eigenvalue problem if you pass a 2D array $\mathbf{B}$ as the second input (if that second input is omitted, the eigensolvers solve the ordinary eigenvalue problem, as described above).

Here is an example program for solving a generalized eigenvalue problem:

from scipy import *
import scipy.linalg as lin

A = array([[1,3,1],[1, 3, 4],[2, 4, 2]])
B = array([[0,2,1], [0, 1, 1], [2, 0, 1]])

lambd, Q = lin.eig(A, B)

## Verify the solution for first generalized eigenvector:
lhs = dot(A,Q[:,0])             # A . x
rhs = lambd[0] * dot(B, Q[:,0]) # lambda B . x

print(lhs)
print(rhs)

Running the above program prints:

[-0.16078694+0.j -0.07726949+0.j  0.42268561+0.j]
[-0.16078694+0.j -0.07726949+0.j  0.42268561+0.j]

The Hermitian eigensolvers, eigh and eigvalsh, can be used to solve the generalized eigenvalue problem only if both the $\mathbf{A}$ and $\mathbf{B}$ matrices are Hermitian.

Computational physics notes | Prev: Gaussian elimination Next: Finite-difference equations